[카테고리:] 과학기술

고전 물리학에서 빛은 전자기파의 일종이며 양자역학에서는 광자라는 기본입자 중에 하나로 간주한다. 그러므로 빛의 속도라는 것은 전자기파의 전파 속도나 광자의 이동 속도로 간단히 정의할 수 있다.

빛의 속도는 물리 상수의 하나로, 중력 가속도 상수 G처럼 불변의 물리량 이며, 왜 그 값인 지 알 수 없고 측정에 의해서 얻어지는 상수이다. 뭔가의 속도라고 하지만 그 의미는 그리 간단치 않다. 여기서는, 그 의미를 해석하기 보다는 과거로 부터 지금까지 빛의 속도를 구하기 위한 과학자들의 노력과 참신한(당시엔…) 아이디어를 소개해 보려고 한다.

참고로 현대의 정밀도로 측정된 빛의 속도는 299,792,458 m/s 이다.

가끔 궁금해서 찾아보는데, 자꾸 잊어버려서 여기에 정리해 놓습니다. 읽어도 이해가 안 되면 잘못 정리된 것이니, 댓글에 이해가 안되는 부분을 남기시면 보충하겠습니다.

2023.10 윤지평

목성과 이오 위성의 이클립스 주기를 사용한 빛의 속도 측정 (1670 Ole Romer, Hoygen et al.)

지구, 태양, 목성 그리고 목성의 위성인 이오와 관계에서 이오가 목성의 그림자에 들어갔다 나오는 주기의 변화를 사용하여 빛의 속도를 계산하는 방법이다. 당시에는 이들 태양, 행성, 위성 간의 거리의 비율은 짐작하더라도 절대값을 알지 못했기 때문에 빛의 속도에 대한 절대 값을 구해낼 수 없었다. 단, 현대적인 측정 치와의 비교를 위하여 그 거리를 대입하여 산출하였다.

이 당시 과연 빛에 속도가 있을까? 빛의 속도는 무한대가 아닌가 하는 생각을 하는 사람들이 대다수 였고, 로머 Romer가 이오의 이클립스 주기를 관찰한 것은 빛의 속도를 측정하기 위함이 아니었다. 예상하지 못한 주기를 갖는 편차를 고민하다가 빛에도 속도가 있는 것은 아닐까 라는 가설을 떠올리게 된 것이다. 그의 빛에 대한 생각과 속도 계산은 대다수의 학자들에게 환영받지 않았지만, 당대의 카시니, 호이겐스, 뉴톤과 같은 과학자들에게 지지를 받게 되었다.

이오에서 지구까지 오는 빛의 속도 계산

계산을 위한 기본 전제는,

• 태양에 대한 지구와 목성의 태양 공전 궤도는 완전 구형이고 주기가 일정하다. 목성에 대한 이오의 공전 궤도도 일정하며 1.76925 일이다.
• 임의의 시간에 지구와 목성 사이의 거리(단위 AU, 지구와 태양과의 거리는 1 AU) 를 알 수 있다.

지구에서의 관측 데이터는 다음과 같다,

• 관측(1): 9월 11일 2:59:30 이오가 목성의 그림자에 가려졌다. 이 때, 지구와 목성 사이의 거리는 5.26127 AU 이다.
• 관측(2): 11월 9일 00:58:30 이오가 목성의 그림자에 가려졌다. 이 때, 지구와 목성 사이의 거리는 4.14690 AU 이다.

관측 (1)에서 관측 (2)까지의 날 수는 대략 85일 이므로, 이오의 공전주기로 나누면,

• 85/1.76925 = 48.044 회
• 실제 공전 횟수: 48 회

두 관측 시점 사이에 위성 이오의 실제 공전 횟수는 48회가 일어났다고 할 수 있다. 다시, 위성 이오 입장에서 48회의 공전에 필요한 시간과, 지구에서 관측된 시간을 계산해 보면,

• 이오가 1~48번째 이클립스에 걸린 실제 시간: 48 x 1.76925 = 84.924 일
• 두 관측 간의 시간 차 : (11월9일 00:58:30)-(9월11일 2:59:30) = 84.916일
• 84.924 일 – 84.916 일 = 0.008 일 (실제 간격과 관찰된 간격의 시간 차)

실제와 관측 시간 간격 사이에는 0.008일 즉, 약 691초의 차이가 있음을 알 수 있다. 왜? 이 시간 차이는 두 번의 관측 시점에서 변화된 지구-목성의 거리 차이를 빛이 더 이동하는데 걸리는 시간이라고 볼 수 있다 (여기서는 거리가 가까워진 경우이지만 상관없다). 두 관측 시점에서 지구-목성의 거리가 동일하다면 실제 시간과 지구에서의 두 관측시간 차이는 없었을 것이다. 결국 빛의 속도를 계산하면,

• 두 관측시점 간 지구-목성의 거리 변화: 5.26127 AU – 4.14690 AU = 1.11437 AU
• 실제 시간과 관측 시간 차이: 691초
• 1 AU: 149,600km (당시에는 몰랐던 값) 으로 빛의 속도를 계산해 보면;
• 1.11437 AU * 149,600,000 km / 691 sec = 241,258 km/sec

현대의 측정 값에 비교하여 20%의 오차가 있지만, 빛에도 한정된 속도가 있다는 하나의 단단한 증거가 발견된 것이며 과학계에 큰 반향을 일으킨 측정 결과이다.

지구의 공전 속도에 기인한, 먼 천체의 광행차를 사용한 빛 속도 측정 (1730 James Bradley)

광행차 Stella Aberration란 지구의 공전 운동으로 별 빛이 기울어져 관측되는 현상을 이야기 한다. 바람 없는 날 장대비가 쏟아 질 때, 움직이는 차창에 빗물이 사선으로 떨어지는 현상과 동일하다. 먼 천체의 빛은 장대비고 그 속을 달리는 차량이 지구라고 생각하면 된다.

광행차 현상

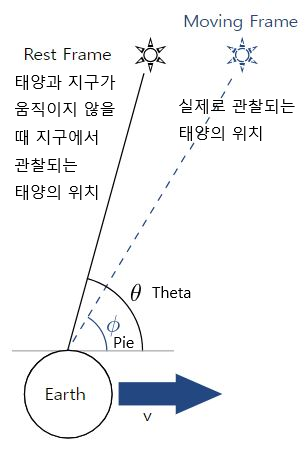
태양과 지구의 거리도 빛이 8분이나 걸릴 만큼 상당히 떨어져 있어서 광행차가 나타난다. 그림에서 Theta는 지구가 정지해 있을 경우 태양이 관찰되어야 하는, 계산 가능한 각도이다. 이에 반하여 Pie는 관찰되는 각도이다. 지구의 공전 속도에 영향을 받는다. 이 공전 속도도 알려진 값이다.

• 지구를 원점으로 하는 xy 좌표계를 생각해보자.
• 태양에 지구로 오는 빛 속도의 x와 y 성분을 각각 v_x, v_y라고 하고 지구의 공전 속도를 v라고 하면,
• tan(Pie) = v_y/(v + v_y), 분모 분자를 c로 나누면
• tan(Pie) = sin(Theta)/(v/c+ cos(Theta)) — 광행차 식(1)
• 위 식에서 c 값은 구해야 하는 것이고, 이 외에는 모두 관찰되거나 계산 가능한 수이므로 빛의 속도 c의 계산이 가능하다.

James Bradley의 빛 속도 계산

1725년 James Bradley는 용자리의 가장 밝은 별 감마 드라코니스를 관찰하면서 1년 단위로 측정각이 사인파의 모양으로 바뀌는 것을 알게 되었다. 친구인 Molyneux와 여러 가지 가설들-지구 자전, 대기의 주기적인 움직임, 망원경의 문제 등-을 검토했지만 설명하지 못했고, 결국 광행차 현상 임을 확신하게 되어 1729년 발표하였다.

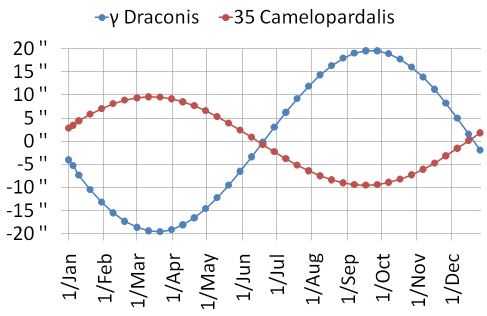
James Bradley는 감마 드라코니스 외에도 10여 개의 다른 별들의 광행차를 관측한 후, 지구 공전에 의한 광행차 각을 약 20.2″ (약 1/3도), 0.00009793 rad 임을 알게 되었다. 즉, 위의 광행차 식 (1)에서,

• Pie = 0.00009793 rad
• Theta = 90도
• 지구의 공전 속도 v = 29.76km/s

위에서 구한 광행차 식(1)에 위의 데이터를 대입하면 빛의 속도 c = 295,000km/s 가 계산된다. 오차의 크기가 1%에 근접하고 있다. 상당히 나이스한 접근이었으며지구는 공전 뿐만 아니라 자전하는 운동이 있고 또 태양계는 은하의 중심을 돌고 있으므로 여러 광행차의 요소들이 배제 되어야 하며, 광행차 각의 크기가 아주 작아서 관측의 오차에 민감하지만 오차 1%는 놀라운 결과이다 (당시에는 정답을 모르니 오차가 얼마인 지도 몰랐겠지만…).

회전하는 톱니 바퀴와 먼 곳의 반사경을 사용한 빛의 속도 측정 (1850 Louis Fizeau)

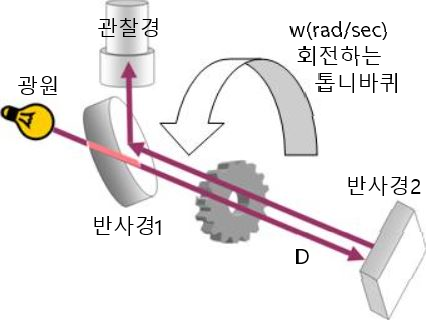
프랑스 물리학자 피조 Hippolyte Fizeau 는 오랜 기간 빛의 갑섭 효과를 연구하였고 일찌기 적색편이와 전자기파의 존재를 예상한 인물이다. 피조는 빛의 속도를 구하기 위하여 회전하는 톱니바퀴를 사용하였다 (바로 위 그림 참조).

그림에서 광원을 떠난 빛은 반사경1을 지나 w 속도로 회전하는 톱니바퀴를 지나 (일부는 막히겠죠). 통과한 빛은 거리 D를 지나 반사경2에서 반사된다. 반사된 빛은 다시 회전하는 톱니바퀴로 돌아온다. 이 때, 빛이 들어온 톱니의 다음 톱니를 돌아온 빛이 지날 수 있도록 속도 w를 적절히 조정한다. 당시 실험 값은 다음과 같다;

• 톱니바퀴와 반사경2 사이의 거리: 8,633m
• 톱니갯수: 720개
• 톱니바퀴의 속도: 25.2 rps (되돌아 온 빛이 통과할 수 있도록 조절된 값)
• 톱니 하나가 지나는 시간 T : 1 / (720 x 25.2)
• 톱니 하나가 지나는 시간 동안 빛이 진행된 거리 2 x D : 19,266 m

2D/T가 빛의 속도이므로 계산하면, 313,274,304 m/s 이다. 이것의 현대 측정치에서 5% 정도의 오차를 갖는다.

회전하는 반사경과 먼 곳의 반사경을 사용한 빛의 속도 측정 (1862 Leon Foucault)

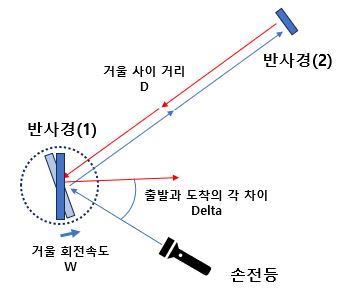
회전하는 반사경(1)에 레이저 포인트나 손전등을 비추면, 반사경(1)에서 반사된 빛이 360도 사방으로 돌아가며 비추게 될 것이다. 빛이 도달하는 임의 한 곳에 또 다른 반사경(2)이 있어서 들어오는 빛을 그대로 반사하여 중앙으로 되돌려 보낼 수 있도록 각도가 설정되어 있다. 반사경(1)이 회전하지 않는다면, 반사경(2)에서 돌아 온 빛을 레이저나 손전등 방향으로 반사하게 되지만 반사경(1)은 회전 중이므로 방향이 Delta 만큼 틀어진다. 빛의 속도가 빠르면 조금 달라질 것이고 속도가 느리다면 크게 달라진다. 빛의 속도를 구해보자.

반사경(1)과 반사경(2)와의 거리: D (m)
반사경(1)의 회전속도: W (rad/sec)
회전에 의하여 틀어진 각도: Delta (rad)
빛의 속도: c (m/sec)

라고 할 때, 빛이 반사경(1)->반사경(2)->반사경(1)의 경로로 돌아온 시간은 회전하는 반사경이 Delta 만큼 틀어진 시간이므로, 이 시간을 T라고 하면,

T = Delta/W

이 때, 빛이 이동한 거리는 2D 이므로 빛의 속도는,

c = 2D/T = 2DW/Delta

로 계산된다.

오차는 주로 반사경(1), 반사경(2) 사이의 거리, 반사각의 차이 Delta의 측정 오류에 기인한다. 당시에 이 방식으로 측정된 빛의 속도는 298,000 km/s 이며, 이는 현재 측정 값과 비교해 볼 때 0.6%의 오차를 갖는다. 와우!

맥스웰의 전자기 방정식을 사용한 전파의 속도 계산 (1910 Rosa, Dorsey)

전하 간의 당기는 힘과 미는 힘의 관계를 기술한 가우스의 법칙 (Gauss’s Law), 코일 사이로 자석을 흔들면 전기장 E가 생긴다는 페러데이의 법칙 (Faraday’s Law), 흐르는 전류 주변으로 자기장이 생기는 현상의 암페어 법칙 (Ampere’s Law)등을 합쳐 일반화 한 4개의 아름다운 수식을 맥스웰 방정식이라고 한다.

4개의 방정식은 정지한 전하, 움직이는 전하(전류), 전기장 E, 자기장 B 사이의 관계를 기술한다. 이 식에는 실험적으로 측정한 두 개의 상수가 존재하는데 바로 전기장 변화와 자기장의 비례 상수, 즉 유전율 e₀와 전류, 전기장의 변화와 전기장의 비례상수인 투자율 u₀ 이다. 이 때, 맥스웰 방정식은 다음과 같다;

맥스웰 방정식은 빛의 속도를 정의한다?

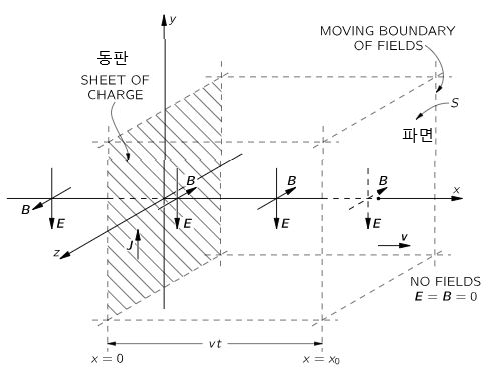
무한대의 동판이 있다고 하고 이것을 z-y 평면에 두고, 이 평면에 직각으로 x축이 있는 3차원 좌표계를 상상하자 (그림 1 참조). 그리고, 동판에 y 방향으로 전류J를 흘리면;

1. 동판의 앞과 뒷면의 표면에는 전류의 수직 방향으로 전류 J의 크기에 비례하는 자기장 B가 발생한다 (암페어의 법칙, 맥스웰 방정식 4번의 오른쪽 첫번째 항).
2. 1 에서 발생하는 자기장의 변화(dB/dt)에 비례하여 전기장 E가 유도된다. (패러데이 법칙, 3번 식의 오른쪽 항)
3. 2에서 유도된 전기장 E의 변화량에 비례하여 다시 B가 유도된다.(암페어 법칙, 맥스웰 방정식 4번식의 오른쪽 두번째 항)
4. 2와 3이 반복되면서 B, E가 직각으로 교차 유도되며 -x와 x,양쪽 방향으로 퍼져나간다.
5. 퍼져나가는 속도를 v라고 하고 X0의 시간이 흘러 어느 정도 전파가 진행되었다고 하자.

암페어의 법칙 적용

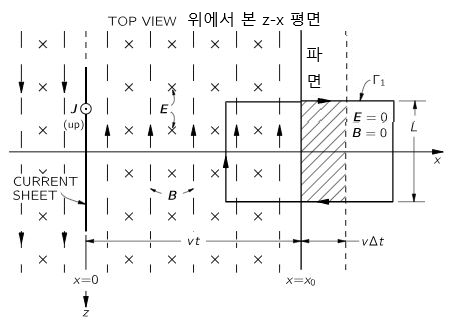
6. 그림 1의 구조를 위에서 바라보면 그림 2와 같다. 그리고 x-z 평면에 파면을 가운데로 하는 한 면의 높이가 L인 직사각형을 생각해보자. 이 직사각형의 면은 E에 수직이고 직사각형의 반은 전자기파가 있고 나머지 반은 아직 전자기파가 없는 상태이다.
   
   전자기파의 속도를 v로 가정했으므로, 맥스웰 방정식 4의 왼쪽 항은 BL 이 되고 오른쪽 항의 첫째 항은 전류가 없으므로 J=0, 두 번째 항, 즉 E의 변화 량은 e₀u₀vLE 이 된다. 그러므로 식 4는 다음과 같다;
   
   B = e₀u₀vE — (관계식1)

페러데이 법칙 적용

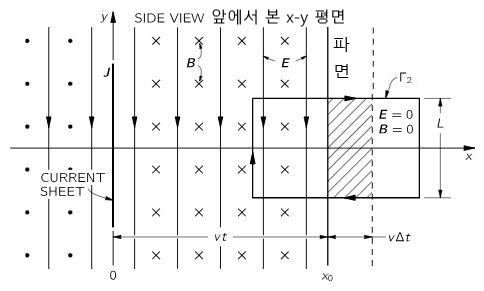
7. 다시 그림 1의 구조를 앞에서 보면 그림 3과 같다. x-y평면에 파면을 가운데로 하고 높이가 L인 정사각형을 생각해보자. 이 정사각형은 B에 수직이고 정사각형의 반은 전가기파가 있고 나머지 반에는 전자기파가 아직 없는 상태이다. 식 3에서 왼쪽 항은 EL이고 오른쪽 항, 즉 B의 변화량은 vBL이 된다. 그러므로 맥스웰 방정식의 3 번식은 다음과 같다;
   
   E = vB —(관계식2)
   
8. 관계식 1과 관계식 2가 동시에 만족하려면, 전자기파의 전파 속도 v는 다음과 같아야 한다;
   
   v = 1/srt(e₀u₀)
   
   전파의 속도를 구해는데… 빛의 속도와 같다네 ㄷㄷㄷ. 알려진 e₀ 와 u₀ 값을 대입하여 속도를 구하면 299,788 km/s이다.

전자기장의 전파 속도와 빛의 속도

놀랍게도, 계산된 1/srt(e₀u₀)는 측정된 빛의 속도와 동일하다. 전기장, 자기장, 전하의 관계 식에서 실험적으로 나타난 두 개의 비례 상수를 곱하여 역수를 취하면 빛의 속도 제곱값이 나온다니… 이러한 결과는 빛도 전자기파의 일종이라는 사실이 널리 인정되는 계기가 된다.

레이저와 간섭계를 사용한 빛의 속도 측정 (1973 Evenson et al)

1960년 휴즈 연구소 Hughes Research Lab. 에서 최조의 레이저 발생기가 만들어 졌다. 레이저는 결이 맞는 단일 파장의 빛을 내는 특징이 있다. 1973년 이벤슨은 이러한 특징을 이용하여 빛의 속도를 측정하였다.

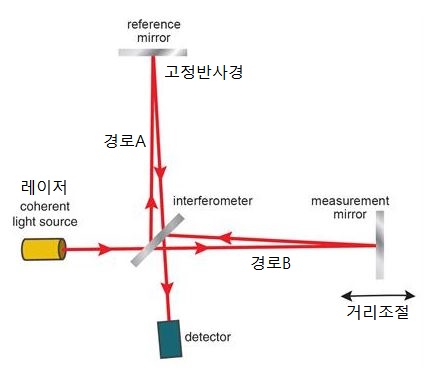
엄밀하게 이야기하면 빛의 파장 길이를 알아내는 방법이라고 볼 수 있으며 이러한 장치를 간섭계 interferometer 라고 한다 (위 그림). 레이저의 빛은 두 개로 나누어 길이가 다른 경로 (경로A, 경로B)를 거쳐 한 곳으로 모인다. 빛은 파동의 특성을 갖기 때문에 한 곳에 모인 곳에서는 두 개의 경로 길이에 따라 두 개의 파장이 보강 constructive, 상쇄 destructive 혹은 그 사이 상태가 된다. 이러한 현상을 간섭 현상이라 한다.

두 개의 경로 중 하나의 경로의 거리를 조절하여 보강과 상쇄가 되는 거리를 찾아내면 바로 빛의 파장 거리를 알 수 있는 원리이다. 레이저 빛의 주파수 f 는 정해져 있으므로 그 빛의 파장 거리를 알면 속도를 알 수 있다.

이러한 원리로 이벤슨 Evenson이 측정한 빛의 속도는 299,792,457.4 m/s 로써 현대의 정밀한 측정값에 비하여 오차 1 m/s 이내의 값이다.

완전히 동일한 방법으로 중력파를 검출하였다. LIGO는 “Laser Interferometer Gravitational wave Observatory 레이저 간섭 중력파 관측” 의 약자로 기본적으로 위 그림의 간섭계와 동일하다. 경로 A와 경로 B를 직각으로 위치 시키고 하나의 길이는 4km 정도 이다. 경로는 완전 진공으로 유지 되어야 한다. 중력파는 공간의 길이가 변경되는 파동이므로 LIGO를 지날 때 간섭무늬가 나타난다.

전자렌지와 초콜릿을 사용의 빛의 속도 측정 (2023 Youtube)

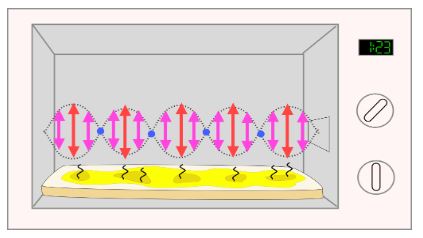
전자 렌지를 켜면 위의 그림처럼 2.45GHz의 전자기파가 정상파를 이룬다. 그림처럼 음식판이 회전하지 않으면 골고루 익지 않고 강한 부분만 익게 되어 반파장의 길이를 알 수 있다.

전자 렌지에 회전하는 판을 제거하고 될 수록 넓은 초콜릿 판을 넣고 짧은 시간 동안 가열하면 위 그림과 같이 반 파장 너비의 자욱이 나타난다. 정밀하진 않지만, 약 6.3cm 간격의 무늬가 나타나므로 파장의 길이는 그 두 배인 0.125m 라고 볼 수 있다. 전자 렌지에는 2.4GHz, 즉 1초에 2.45G 번 진동하는 전자기파를 사용하며 한 번 진동할 때마다 0.125m를 이동하는 것이므로 이 두 숫자를 곱하면,

2,450,000,000m x 0.125m = 306,250,000m/s 로 계산되며 현대의 측정 값에 비하여 2%정도의 오차를 갖는다. 대단 대단…

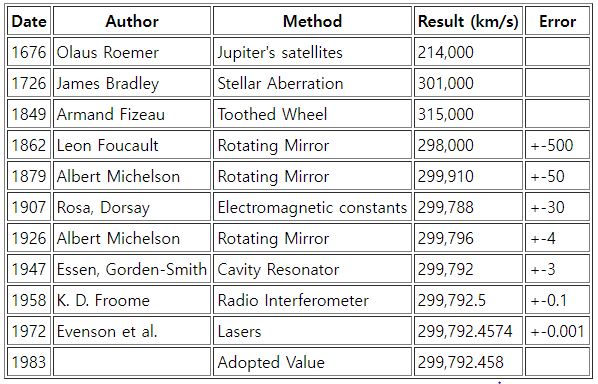
빛의 속도 측정 연대기